Solving Sliding Tile Puzzles Using A* Algorithm

Overview of the Sliding Tile Puzzle

The Sliding Tile Puzzle is a classic problem in artificial intelligence and computer science. It consists of a grid of numbered tiles with one tile missing, allowing the player to slide the adjacent tiles into the empty space. The objective is to arrange the tiles from a given initial configuration into the goal state using the fewest possible moves. Each move consists of swapping any adjacent tile (up, down, left, right) with the empty slot.

The complete code of each algorithm and method implemented in this article is available here along with all the final solutions.

Puzzle Setup 

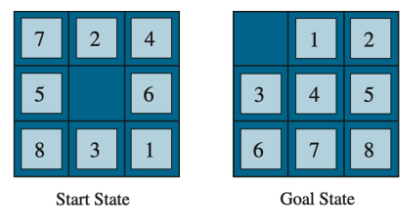
For our project, we'll be working with the 8-tile puzzle, which is a 3x3 grid containing tiles numbered 1 to 8 and a single empty space (represented by 0 in the code). The figure below displays the start and goal states of the tiles. When selecting these states, keep in mind that not all configurations are solvable from a given initial state. Therefore it is important to verify whether a solution exists and our code should be able to output this message in such cases.

Solution Approach

When tackling the Sliding Tile Puzzle, there are several algorithms we can consider, such as Breadth-First Search (BFS), A*, and Iterative Deepening A*. For our solution, we will be using the A* algorithm due to its effectiveness in finding the shortest path in a search space. If you want more details on search algorithms, including A*, check out my previous project on maze search.

We'll use the number of misplaced tiles as the heuristic estimate of each path. Looking at the start state there are 4 possible moves and each of the paths has a heuristic cost of 8 as  

def heuristic(state, goal):
    num_displaced = 0
    for i in range(3):
        for j in range(3):
            if state[i][j] != 0 and state[i][j] != goal[i][j]:
                num_displaced += 1
    return num_displaced

Applying A* on Sliding Tile Puzzle

Initialization: Start with the initial configuration of the puzzle. Initialize the priority queue with this state and an empty dictionary to track the cost of reaching each state.

Expand the nodes: Expand the current state by generating all possible successor states through valid tile moves (up, down, left, right).

def get_paths(state):
    paths = []
    for i in range(3):
        for j in range(3):
            if state[i][j] == 0:
               zero_pos = (i, j)

    # Action: Up, Down, Left, Right    
    for direction in [(-1, 0), (1, 0), (0, -1), (0, 1)]: 
        i, j = zero_pos[0] + direction[0], zero_pos[1] + direction[1]
        
        if 0 <= i < 3 and 0 <= j < 3:
            new_state = [list(row) for row in state]

            # Action = swap blank tile
            new_state[zero_pos[0]][zero_pos[1]], new_state[i][j] = new_state[i][j], new_state[zero_pos[0]][zero_pos[1]]
            paths.append((tuple(map(tuple, new_state)), direction))
    return paths

Evaluate and queue: For each successor state, calculate the cost g(n) and the heuristic h(n). If the new path to this state is shorter than any previously found, update the cost and queue the state with its f(n) value.

Check for goal state: Continue this process until the goal state is reached or the priority queue is empty (indicating no solution).

Path reconstruction: Once the goal state is reached, reconstruct the path from the initial state to the goal state by backtracking through the tracked states.

Conclusion

By leveraging the A* algorithm and its heuristic estimation, we efficiently solved the Sliding Tile Puzzle, demonstrating its effectiveness in finding the optimal sequence of moves to reach the goal state.

The shortest path to the goal state was achieved with a total of 27 steps. If you are interested in viewing the 27 steps taken by the algorithm then simply run this command "print(path)" on your notebook. 

Interested in seeing the full code and experimenting with these algorithms yourself? Check out the complete code on my Github page.