Mastering Maze Search - BFS, Dijkstra, A* Algorithms 

Overview of Maze-Solving Algorithms

Maze-searching algorithms are fundamental techniques used in computer science and artificial intelligence to find paths through unfamiliar environments. In this project, we will dive deep into three popular algorithms:

• Breadth-First Search (BFS): An unweighted graph traversal algorithm that explores all nodes at the present depth before moving on to nodes at the next depth level.
• Dijkstra's Algorithm: An algorithm to find the shortest path in a weighted graph, by repeatedly selecting the node with the smallest known distance and updating its neighbors.
• A* Algorithm: A heuristic-based pathfinding algorithm that finds the optimal path by combining the actual cost from the start with an estimated cost to the goal, using a priority queue.

The complete code of each algorithm and method implemented in this project is available here along with all the final maze solutions.

Maze Setup

The sample maze dimensions for our example is a 25 x 25 grid with start state defined at (1,1) and goal state selected at (22, 22). Check the visual representation of the maze layout below where the walls are painted in dark green colors and the free spaces are represented with a lighter shade.

One of the key aspects of this setup is the presence of multiple paths from the start node to the goal node. This allows us to observe how each algorithm navigates the maze and chooses its route. In scenarios where there is no possible path to reach the goal state, it will return a message indicating the issue.

Solving the Maze Using Breadth-First Search (BFS)

BFS starts at the root (or start node) and explores all neighboring nodes at the present depth prior to moving on to nodes at the next depth level. This process continues until the goal node is found or all nodes are explored. Here's a step-by-step breakdown of the BFS algorithm:

1. Initialization:

   • Enqueue the start node and mark it as visited.
   • Initialize an empty queue to keep track of nodes to be explored.

2. Exploration:

   • Dequeue a node from the front of the queue.
   • For each unvisited neighboring node:
     • Mark it as visited.
     • Enqueue it for subsequent exploration.

3. Termination:

   • If the goal node is dequeued, terminate the search and return the path.
   • If the queue becomes empty without finding the goal node, return a message indicating no path exists.

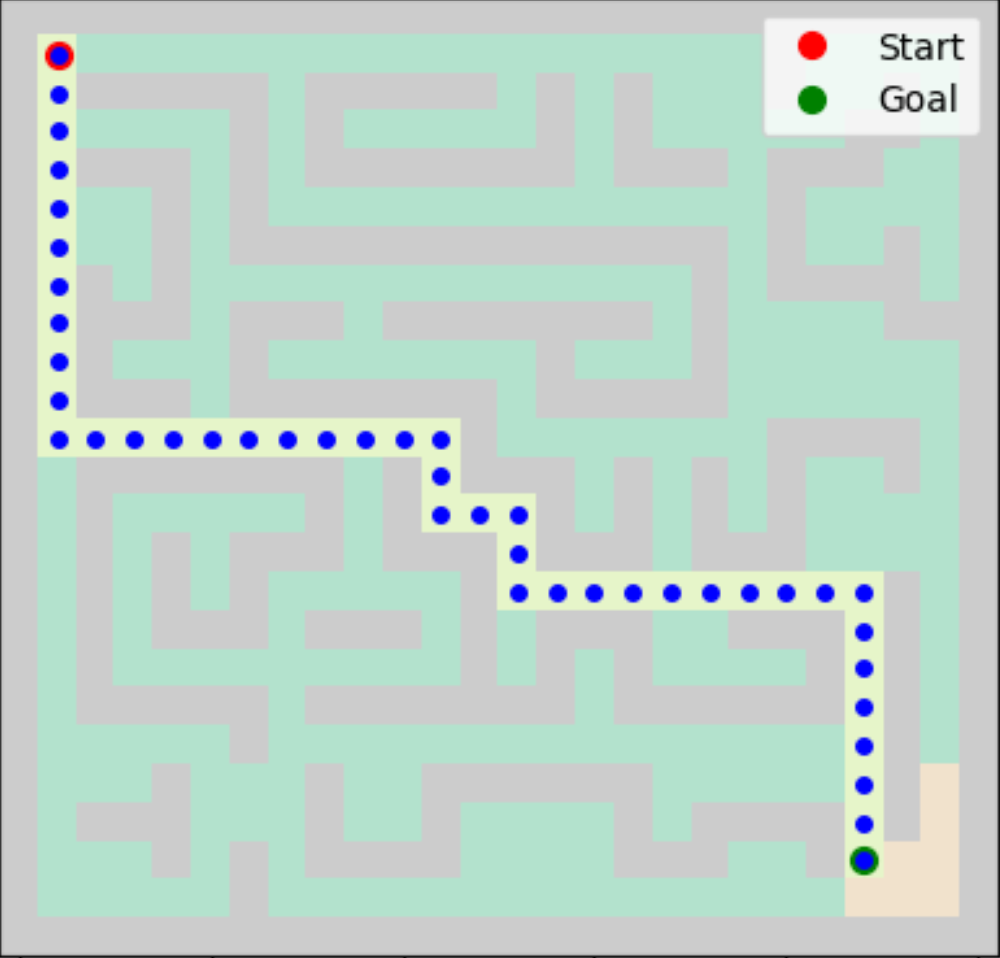
Applying BFS to our chosen maze, we find that BFS successfully discovers the shortest path to the goal node of length 43 steps (displayed using blue circles).

Visualizing the BFS algorithm in action provides a clear understanding of its operation. Starting from the initial node, BFS explores all immediate neighbors, then moves on to the neighbors of those nodes, and so forth. The green portion in the image represents the explored states while the orange nodes are the non-explored states.

In summary, BFS is a powerful and straightforward algorithm for finding the shortest path in unweighted mazes. Its methodical exploration ensures that every possible route is considered, making it a reliable choice for maze-solving tasks.

Solving the Maze Using Dijkstra

Dijkstra's algorithm considers the cost of each move and ensures the least total cost path from the start node to the goal node. It operates by maintaining a priority queue of nodes, where the priority is the current known shortest distance from the start node. Here’s a step-by-step breakdown of Dijkstra’s algorithm:

1. Initialization:

   • Set the distance to the start node to 0 and all other nodes to infinity.
   • Enqueue the start node with a priority of 0 (its distance).
   • Initialize an empty priority queue to keep track of nodes to be explored.

2. Exploration:

   • Dequeue the node with the lowest distance from the priority queue.
   • For each neighboring node:
     • Calculate the tentative distance through the current node.
     • If the tentative distance is less than the known distance, update the distance and enqueue the neighboring node with the new distance.

3. Termination:

   • If the goal node is dequeued, terminate the search and return the path.
   • If the priority queue becomes empty without finding the goal node, return a message indicating no path exists.

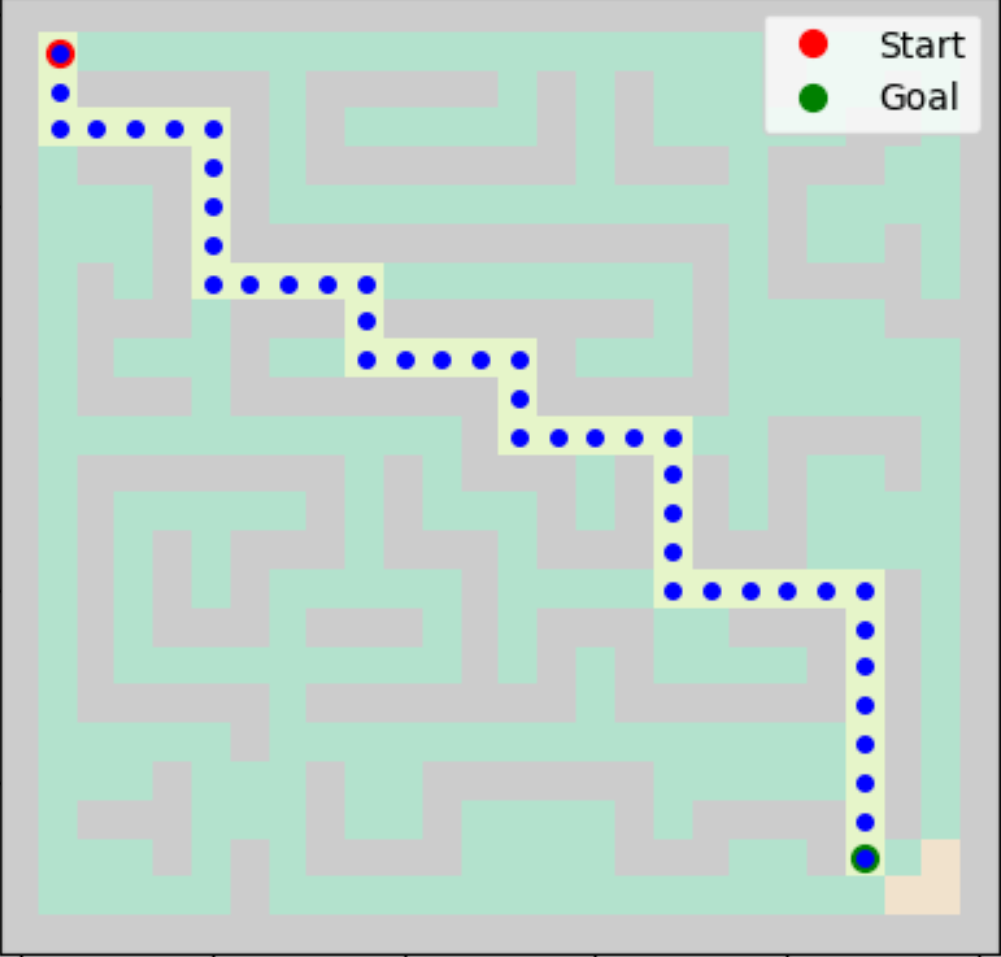
Applying Dijkstra's algorithm to our maze, we observe that it also successfully identifies the shortest path to the goal node with a path length of 43 steps.

Visualizing the path taken reveals its systematic approach to exploring nodes based on their current known shortest distance. Starting from the start node, it evaluates all neighboring nodes, updating their distances and priorities as it progresses. This ensures that the first time the goal node is reached, it is through the path with the least total cost.

In summary, Dijkstra's algorithm is a robust and reliable method for finding the shortest path in weighted mazes. Its consideration of the cost associated with each move makes it an excellent choice for scenarios where different moves have different costs. The results from our maze setup demonstrate its effectiveness in navigating complex pathways and delivering optimal solutions, similar to BFS but with an added layer of cost consideration.

Solving the Maze Using A* Search Algorithm

The A* algorithm finds the shortest path from a start node to a goal node while minimizing the cost of the path. It does this by combining the actual distance traveled from the start node with a heuristic that estimates the distance to the goal node.

A* uses a priority queue to explore nodes based on their combined cost function 'f(n)'. where: 𝑓(𝑛) = 𝑔(𝑛) + ℎ(𝑛)

• 𝑔(𝑛) is the actual cost from the start node to the current node 𝑛.
• ℎ(𝑛) is the heuristic estimate of the cost from the current node 𝑛 to the goal node.

1. Initialization:

   • Set the distance to the start node to 0 and to all other nodes to infinity.
   • Enqueue the start node with a priority equal to its heuristic value $h$.
   • Initialize an empty priority queue to keep track of nodes to be explored.

2. Exploration:

   • Dequeue the node with the lowest 𝑓 value from the priority queue.
   • For each neighboring node:
     • Calculate the tentative 𝑔 value through the current node.
     • If the tentative 𝑔 value is less than the known 𝑔 value, update the 𝑔 value and calculate the new 𝑓 value.
     • Enqueue the neighboring node with the new 𝑓 value.

3. Termination:

   • If the goal node is dequeued, terminate the search and return the path.
   • If the priority queue becomes empty without finding the goal node, return a message indicating no path exists.

Heuristic Calculation

The heuristic function ℎ(𝑛) is crucial for the A* search performance. It provides an estimate of the cost to reach the goal from the current node. For our case, we will use two different heuristic functions:

1. Euclidean Distance:

ℎ(𝑛) = √ {(xgoal - xcurrent)2 + (ygoal - ycurrent)2}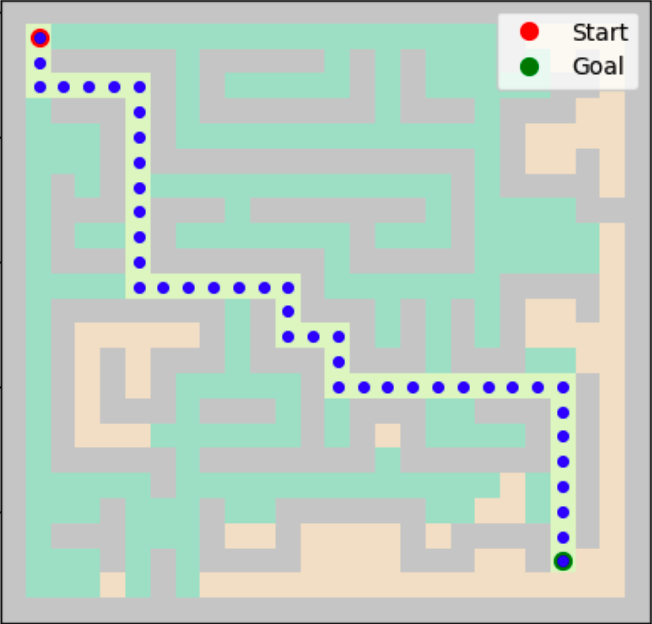

2. Manhattan Distance:

ℎ(𝑛) = |xgoal - xcurrent| + |ygoal - ycurrent|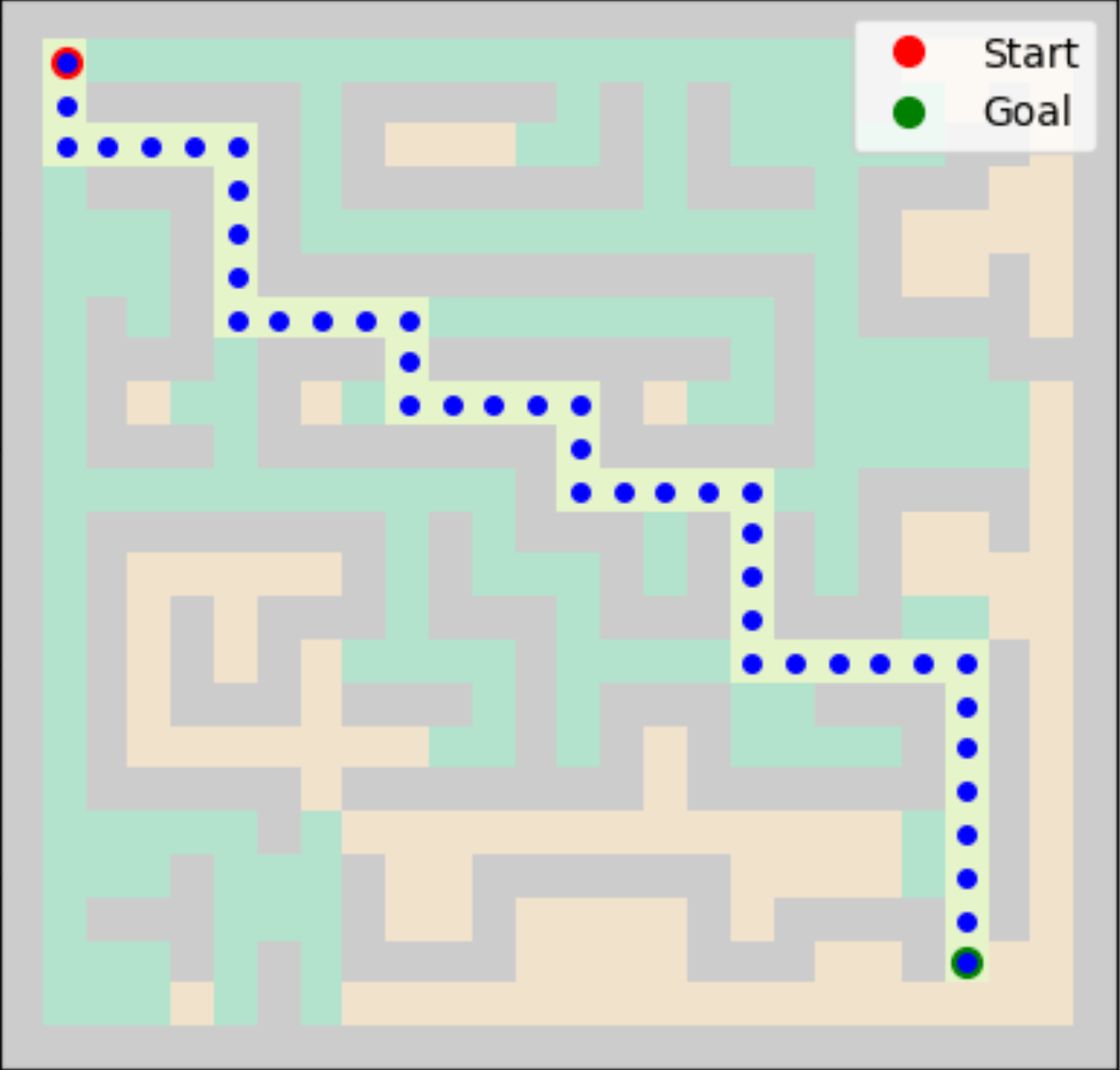

Applying the A* algorithm to our maze with both heuristic functions, we found that it successfully identified the shortest path to the goal node. The path length was 43 steps, consistent with the results from BFS and Dijkstra’s algorithms. However, A* significantly reduced the time taken and the number of nodes explored.

In summary, the A* search algorithm leverages heuristics to guide its search along the least cost path and reduce unnecessary exploration. This demonstrates the algorithm’s strength in balancing optimality and efficiency, making it ideal for maze-solving and other pathfinding tasks.

BFS vs Dijkstra vs A* in maze search

In this section, we will compare the performance of Breadth-First Search (BFS), Dijkstra's algorithm, and A* algorithm (Euclidean and Manhattan) in solving the maze. To provide a comprehensive analysis, we ran each algorithm three times on the same maze provided above but set the start and goal states to random. We collected data on the time taken and the search space explored for each run, allowing us to evaluate the efficiency and effectiveness of each algorithm.

Performance Metrics

1. Time Taken: The total time (in seconds) required for the algorithm to find the shortest path from the start node to the goal node.
2. Search Space: The total number of nodes explored by the algorithm during the search process.

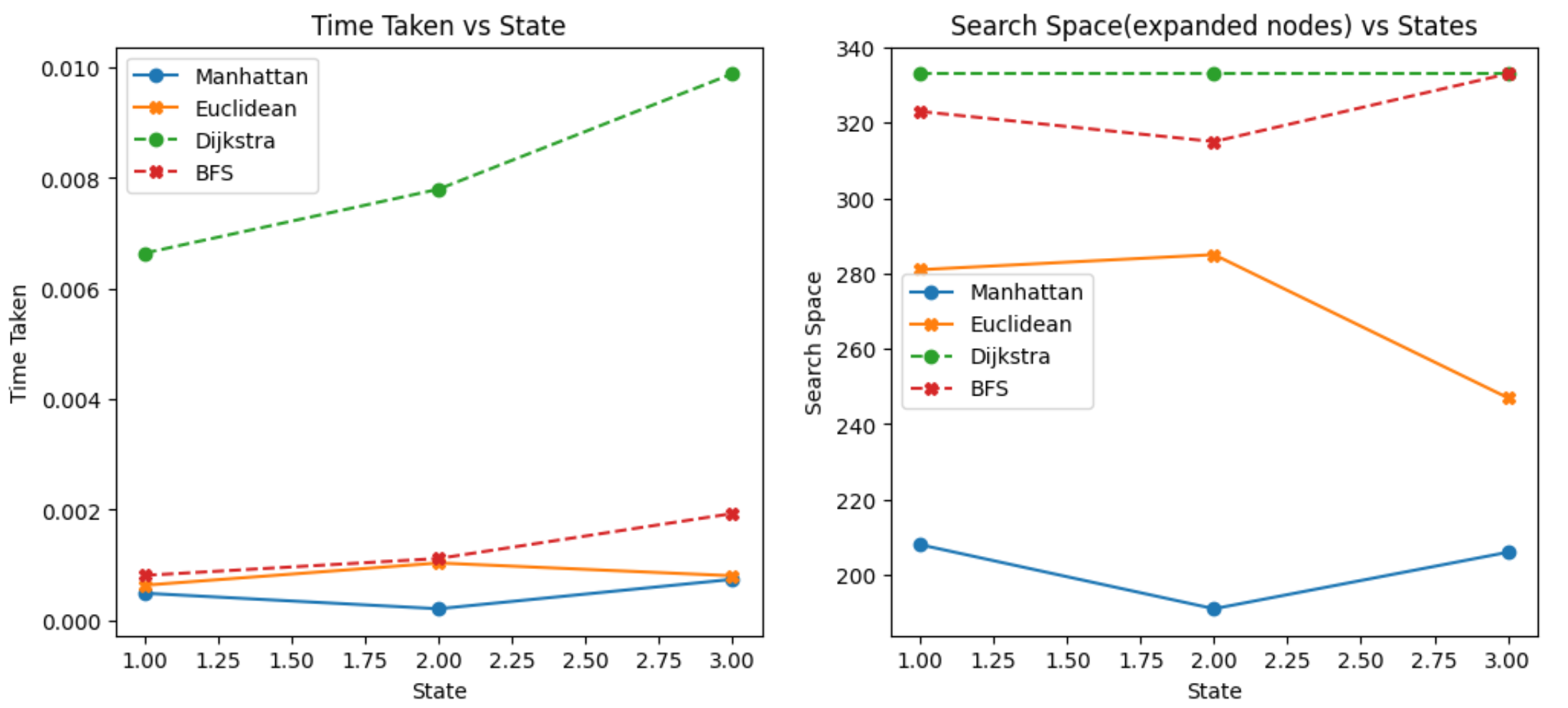
All four methods successfully found the optimal path for each route, given the specified weights.  The extensive exploration (search space) by BFS and Dijkstra is represented by predominantly green areas on their respective solution maze images, indicating a higher search effort and longer execution time. The A* search algorithm, leveraging heuristic guidance, achieves the same optimal paths more efficiently, making it a preferable choice for pathfinding tasks that demand quick and resource-efficient solutions.

Importance of weights in A* Algorithms

In the previous section, we discussed how the A* algorithm efficiently finds the shortest path in less time compared to BFS and Dijkstra's algorithm by leveraging a heuristic function. However, this efficiency can be significantly affected by the choice of weights in the heuristic cost function. Properly tuning the weight is crucial to balance the trade-off between heuristic guidance and actual path cost estimation.

To introduce a weight 𝑊 into the heuristic, the cost function is modified as follows:

𝑓(𝑛) = 𝑔(𝑛) + 𝑊⋅ℎ(𝑛)

• If 𝑊=1: The heuristic and the actual cost are balanced equally, providing an optimal path.
• If 𝑊<1: The influence of the heuristic is reduced, causing the algorithm to behave more like Dijkstra’s algorithm, focusing more on the actual path cost and exploring more nodes.
• If 𝑊>1: The heuristic dominates the actual cost, potentially leading to an overestimation of the path cost, which can cause the algorithm to find suboptimal paths or miss the goal.
• If 𝑊→0: The algorithm disregards the heuristic, effectively transforming into an uninformed cost search. This increases the search space and time as it explores all possible paths based on actual costs.
• If 𝑊→∞: The algorithm relies entirely on the heuristic, disregarding the actual path cost. This will lead to a greedy approach, potentially missing the shortest path and producing results in a shorter time.

Experiment Results:

To understand the impact of different weights on the performance of A* search, we conducted experiments with five different weights (0.1, 1, 5,15 and 40). We measured the time taken (seconds) and the search space explored for each weight, plotted as follows:

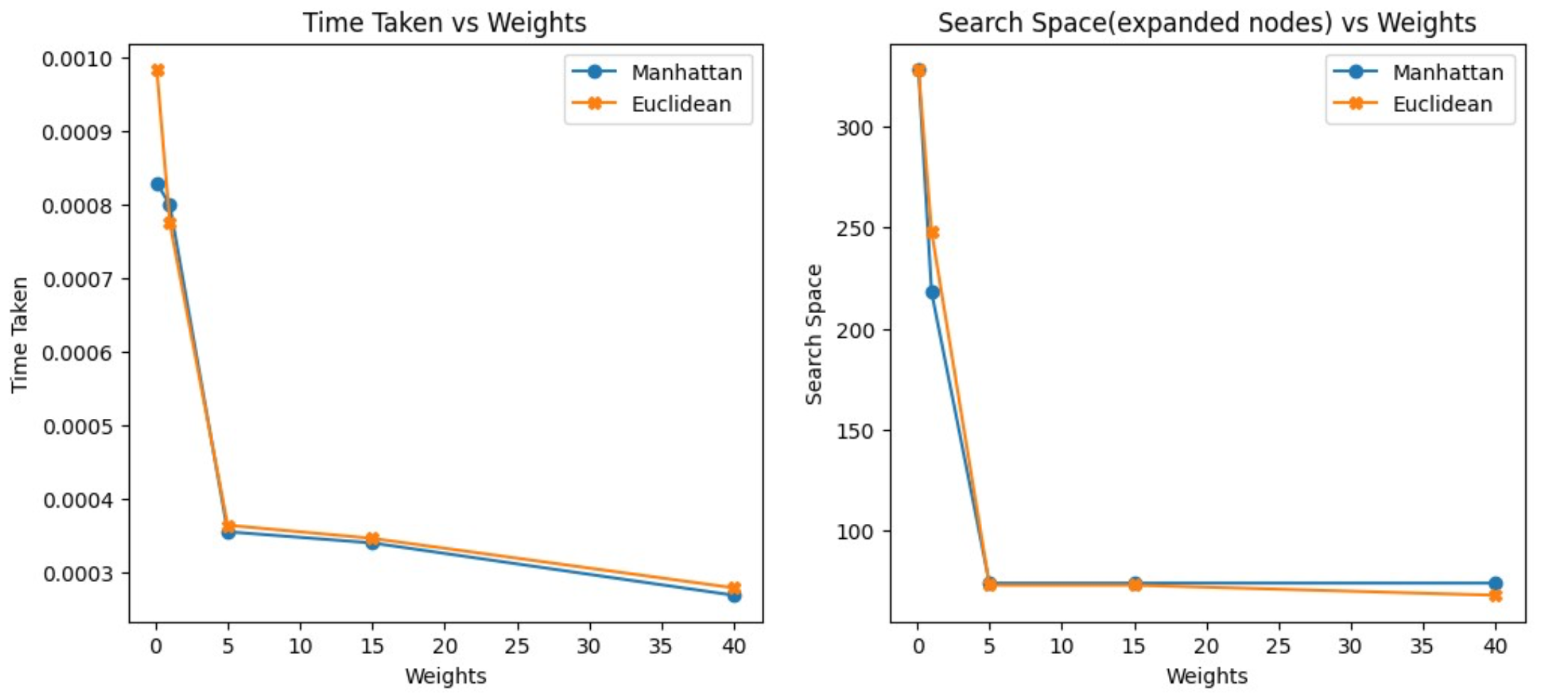
As the weight increases, both the time taken and search space decreases; however, the path might be non-optimal. In that case is there any other way where we can set weight at 1 and still achieve a shorter path at a lower computational cost?

Optimizing Maze Search With Diagonal Navigation

Navigation in real-life environments often includes diagonal paths, which can provide more direct and efficient routes. By incorporating diagonal movement into our maze-solving algorithms, we can significantly optimize the pathfinding process, making it more realistic and efficient.

       

       

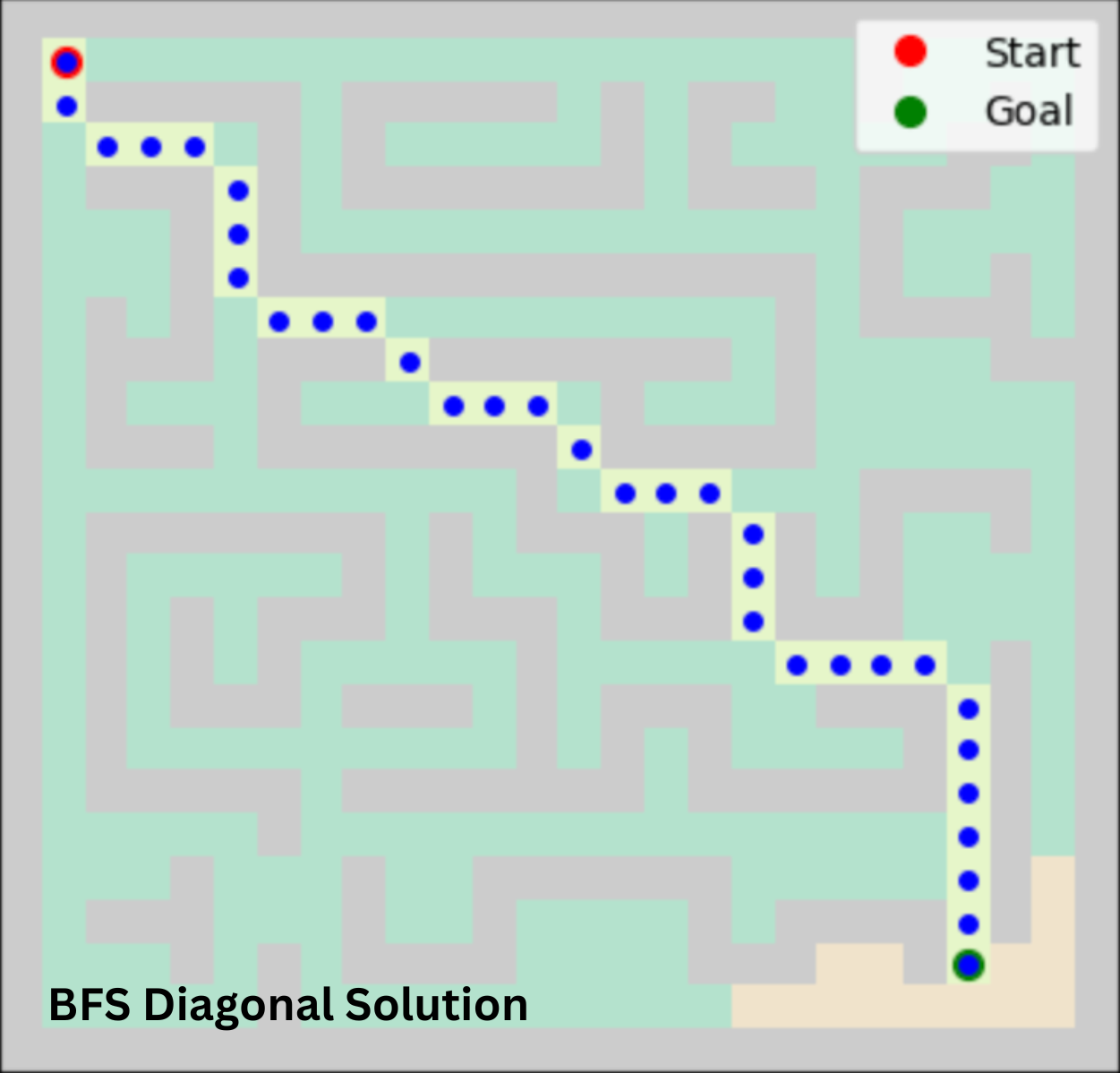
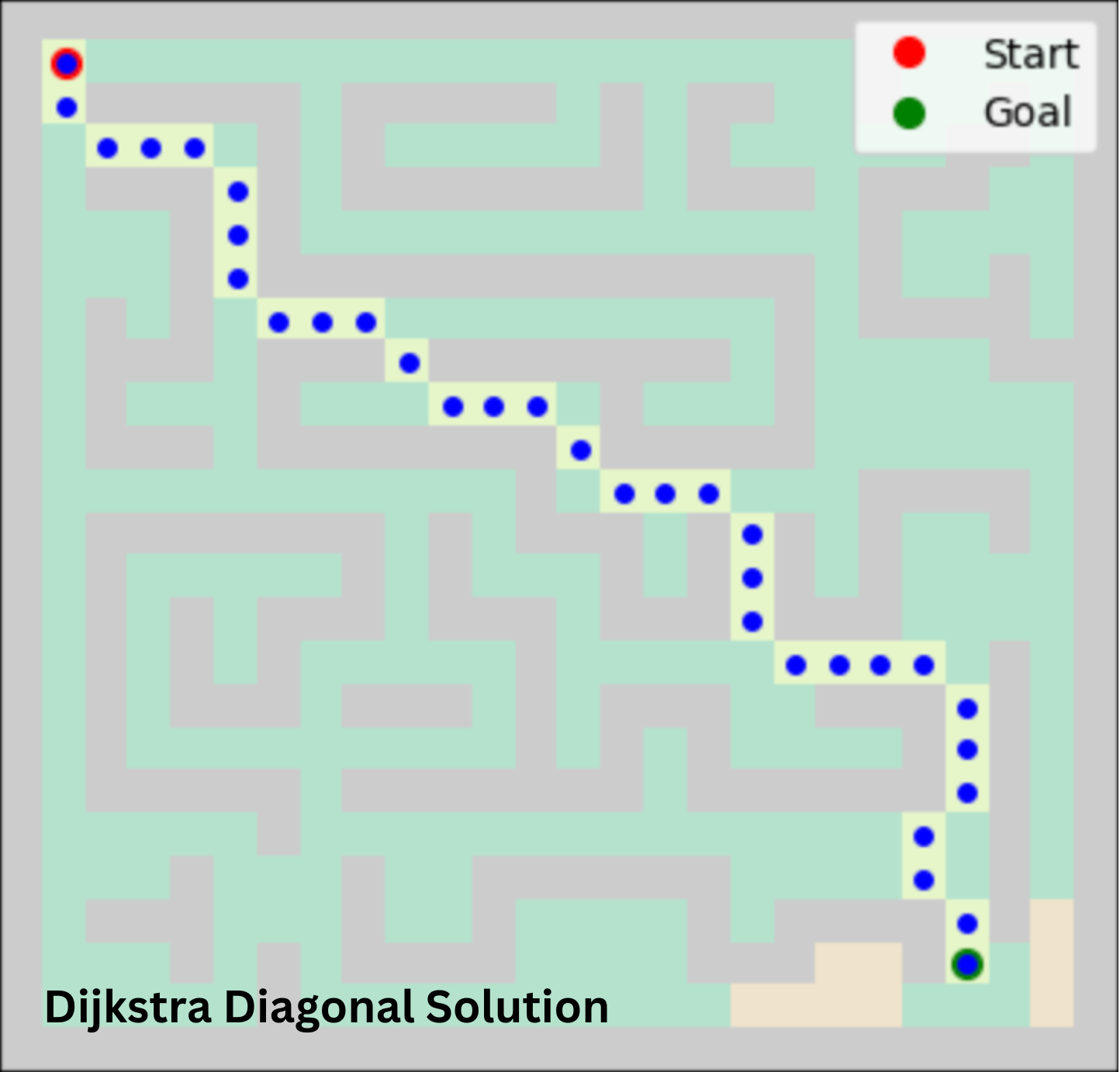
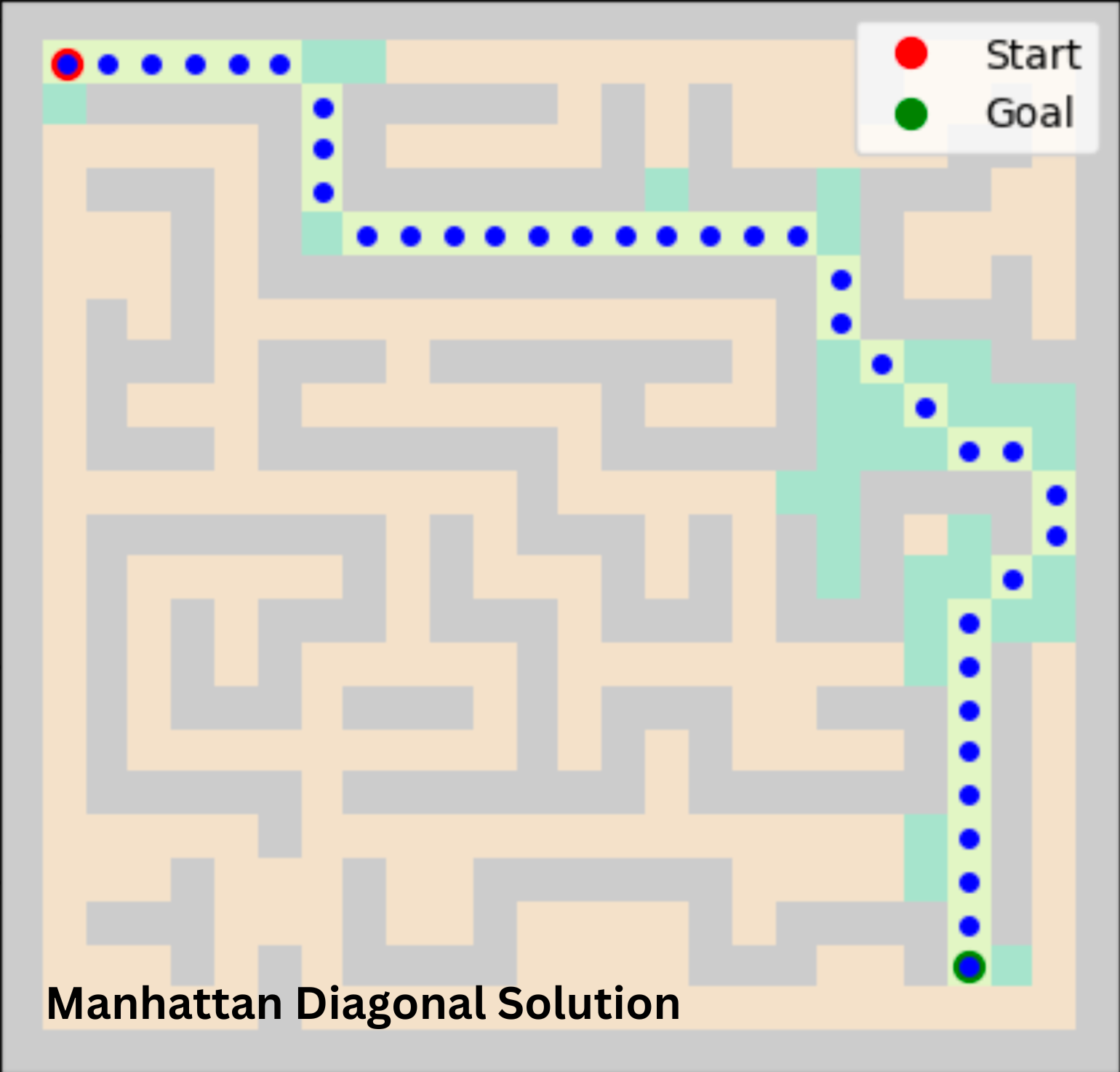
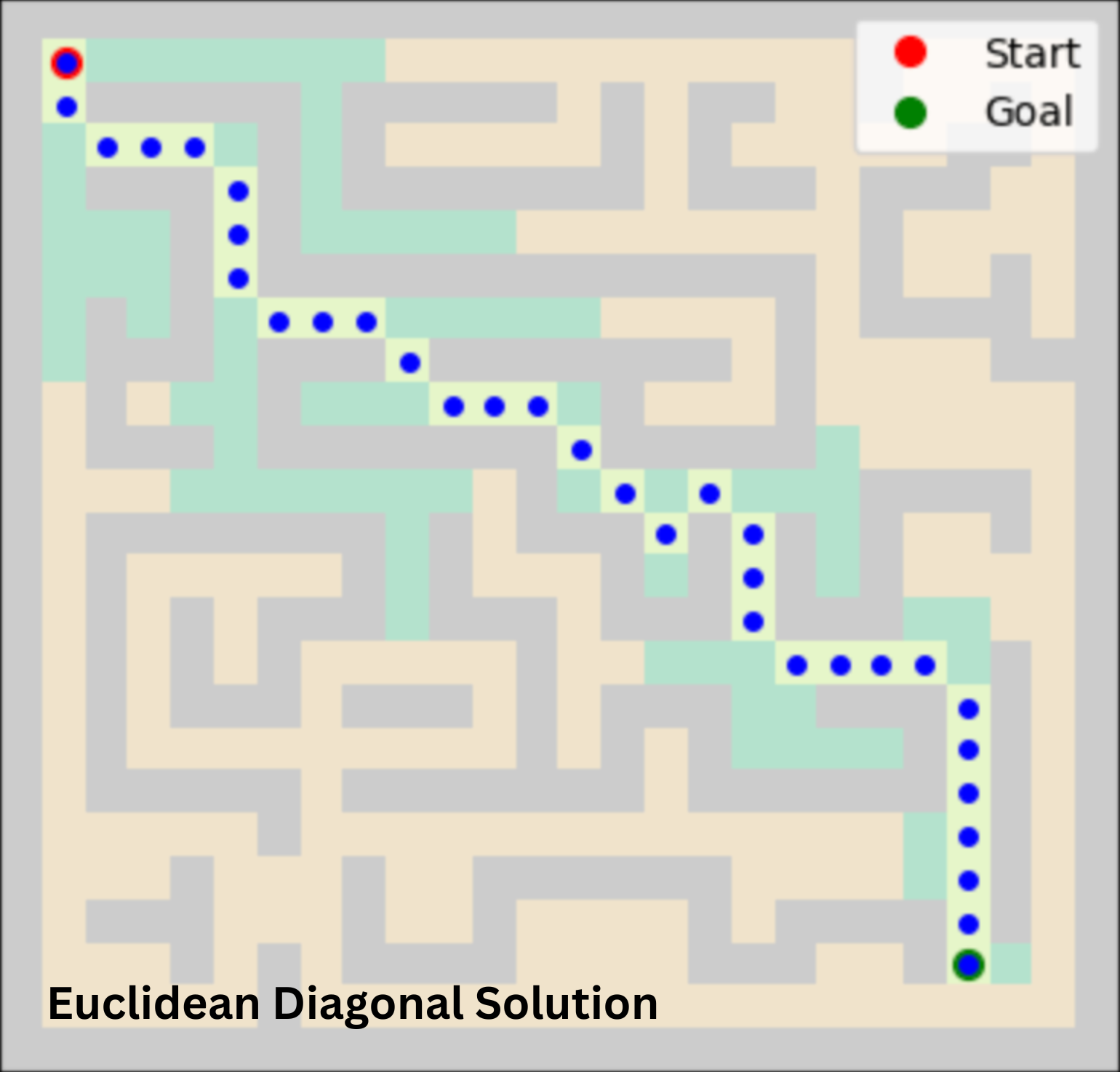
Keeping the maze constant and setting the weight to 1, enabling diagonal movement shortens the optimal path while requiring less search space and time. This difference is especially significant when using a heuristic function. In this approach, the agent has 8 options for every move, which greatly enhances efficiency. The agent can calculate the cost for 8 possible actions simultaneously and select the optimal one for each step. The table below displays a summary of how each algorithm performed.

Algorithm	Path w/o diagonal	Path with diagonal	Search Space w/o diagonal	Search Space with diagonal
Euclidean	43	33	247	108
Manhattan	43	38	218	72
Dijkstra	43	33	330	323
BFS	43	33	326	318

Conclusion

This project explored the maze-solving capabilities of BFS, Dijkstra's algorithm, and the A* algorithm. Furthermore, it highlighted how each algorithm works and compared their performance based on path length, search space, and execution time.

Understanding these algorithms is crucial for various applications, including:

• Robotics: Navigating robots through unknown environments.
• Game Development: Implementing NPC movement and AI behaviors.
• Network Routing: Finding optimal paths in data networks.
• Geographic Information Systems (GIS): Mapping and route planning.

By mastering these algorithms, you'll gain valuable insights into problem-solving strategies that are widely applicable in many fields.

Interested in seeing the full code and experimenting with these algorithms yourself? Check out the complete code on my Github page.